Для определения объема горизонтального резервуара применяется такой же подход, как и при вычислении объема цилиндра. После получения результата объема резервуара целесообразно округлить значение и выбрать наиболее подходящий вариант из стандартного ряда объемов емкостей.
Сколько литров в бочке с маслом?
Важно помнить! При расчетах объема жидкости в резервуаре необходимо учитывать фактический уровень заполнения, а также результаты расчетов должны соответствовать конкретной жидкости, которую вы измеряете.
Объем измеряется в кубических метрах, что является основополагающим фактом в стандартной метрической системе. Длина ребра куба равна одному метру. Обычно данную меру используют, чтобы определить объем резервуара, бочки или цистерны. Расчет объема может быть несколько сложным, так как жидкости чаще всего измеряются в литрах. При проектировании резервуара или цистерны, предназначенной для хранения жидкостей, важно также учитывать массу вещества, что не всегда соответствует количеству литров.
Как известно всем, кто изучал физику в школе, минимальная площадь поверхности для максимального объема наблюдается у сферических емкостей. Однако, поскольку создание сферических контейнеров требует больших затрат и усилий, а также может быть нецелесообразным, большинство производителей выбирают цилиндрические или прямоугольные формы емкостей.
ЦИЛИНДРИЧЕСКИЕ ЕМКОСТИ
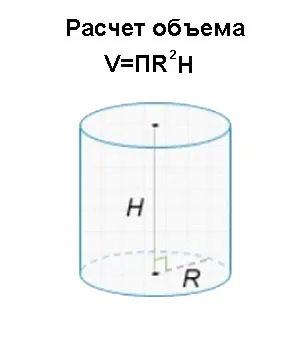
Цилиндрические емкости могут быть установлены как в горизонтальном, так и в вертикальном положении. Объем таких емкостей рассчитывается по формуле V = πr²h, где r — радиус основания цилиндра, h — высота. Для этого необходимо умножить число π, равное примерно 3,14159, на квадрат радиуса и на высоту цилиндра.
Для примера: рассмотрим вертикальный цилиндрический резервуар с диаметром 3 метра и высотой 5 метров. Для вычисления объема резервуара, определим радиус, который составит 1,5 метра, так как радиус — это половина диаметра. Квадрат радиуса равен 2,25. Умножаем: 3,14159 × 2,25 × 5 (высота) = 35,34 м³. Таким образом, рабочий объем данного резервуара составит 35 кубических метров или 35 000 литров (в одном кубическом метре содержится 1000 литров).
На практике размеры резервуара определяются в зависимости от его предназначения. К примеру, горизонтальный резервуар с диаметром 1 метр и длиной 10 метров был бы неэффективен в использовании, ведь его объем составит 7,8 кубических метра. Если нам действительно нужен резервуар такого объема, целесообразнее будет сделать его шире и короче; например, выбрать диаметр 2 метра и длину 3 метра. Таким образом, мы получим тот же объем в 7,8 кубических метра, но с более удобными размерами.
Что понадобится для расчета?
Кроме калькулятора, вам потребуется рулетка, длина которой не должна превышать трех метров.
Первым делом нужно измерить диаметр цилиндрической части резервуара. Это значение легко определить, обнаружив最大альный размер.
Если речь идет о бочке с толстыми стенками, следует учитывать внутренний диаметр, а не внешний.
Если стенки резервуара изготовлены из более тонкого материала, например, нержавеющей стали толщиной до 1 миллиметра, то толщину стенок можно не учитывать.
Измеренное значение диаметра делится пополам; это и будет радиусом бочки. Формула расчета состоит из двух основных шагов:
- Сначала квадрат радиуса умножается на значение числа π, приближенно равного 3,1416. Это число связано с длиной окружности, оно представляет собой бесконечную десятичную дробь, являющуюся иррациональным числом. Результат — это площадь круга, представляющая основание (дно) бочки.
- Далее необходимо измерить высоту бочки и умножить ее на полученную площадь основания. Итогом будет объем емкости. При этом значения должны быть переведены в метры, чтобы результат объема в кубах не оказался нецелесообразно большим.
Если у вас старая бочка с переменным диаметром, подход к расчету будет немного отличаться.
- Сначала измерьте диаметр в верхней части — это будет минимальное действующее значение. В верхней и нижней частях оно будет одинаковым, так как оба дна емкости равны. Делим этот диаметр на два, возводим в квадрат и затем умножаем на значение π.
- Измерив окружность бочки по середине с помощью рулетки, вы получите длину окружности. Разделив ее на π, мы определим диаметр и после снова делим его пополам, чтобы найти максимальный радиус. Из этого радиуса вычитаем толщину стенок (которая указывается непосредственно за счет использования изогнутого материала) — таким образом мы получаем действующее значение радиуса при максимальном значении. Умножив на квадрат максимального радиуса π, мы найдем площадь воображаемой плоскости, проходящей через середину бочки и ограниченной внутренней поверхностью стенок.
- Определяем среднее арифметическое (в квадратных метрах) больших и меньших действующих значений основания емкости, то есть складываем их и делим на два.
- Измеряем (в метрах) высоту и умножаем это значение на среднюю площадь дна емкости.
Полученное значение — это объем полой ёмкости.
Для эллиптической бочки расчет немного отличается:
- Измерьте расстояние между противолежащими точками емкости, которые находятся на эллипсе (что соответствует овалу поперечного сечения). Вы будете работать с двумя значительно различающимися значениями.
- Выясняем среднее арифметическое этих значений, затем делим его на два — получаем радиус.
- Uмеряем высоту и умножаем её значение на квадрат среднего радиуса и число π. Полученное значение в кубометрах будет равно объему овальной емкости.
Хотя термин «радиус» не применим к овалу, его можно определить как среднее значение. Предполагается, что овал представляет собой идеальную кривую, аналогичную сжимаемой или вытянутой окружности.
Объем прямоугольных контейнеров, внутренняя часть которых имеет форму параллелограмма, рассчитывается быстрее, чем у их круглых аналогов. Для вычисления нужно просто умножить длину на ширину и на высоту контейнера.
Что понадобится для расчета?
Вам снова понадобятся калькулятор и рулетка. Длина рулетки может составлять до 3 метров.
Сначала вам нужно измерить диаметр толстой цилиндрической бочки. Это значение также легко определить, заметив его наибольшее значение.
В случае толстостенной бочки обязательно учитывается внутренний, а не внешний диаметр.
Если используется более тонкий материал, толщиной стенок менее 1 мм, то можно пренебречь этой толщиной.
Измеренный диаметр следует разделить на 2 — это будет радиус бочки. Формула расчета состоит из двух основных шагов.
- Квадрат радиуса умножается на число π (3,1415926535…, более приближенное значение – 3,1416). Это число связано с длиной окружности и представляет собой бесконечную десятичную дробь (иррациональная величина). Полученная величина — площадь круга или дна в его реальном размере.
- Измеряем высоту бочки и умножаем её на полученную площадь дна. Это результат, показывающий объем емкости. Значения должны быть переведены в метры, иначе итоговый объем в кубах может оказаться невероятно большим.
Для старинной бочки с переменным диаметром расчет будет отличаться.
- Измеряем диаметр в соответствии с верхней частью, что является наименьшим действующим значением. В верхней и нижней части он будет одинаковым, поскольку оба дна равны. Делим диаметр на два, возводим результат в квадрат и умножаем на число π.
- Определяем длину окружности бочки с помощью рулеточной линейки, обвязывая её вокруг в самой широкой части. Полученное значение делим на число π, чтобы найти диаметр, и затем снова на 2, чтобы определить максимальный радиус. Теперь вычтем толщину стенок, чтобы получить фактический радиус. Умножаем квадрат радиуса на число π, чтобы найти площадь воображаемой плоскости, проходящей по середине бочки и ограниченной внутренними стенками.
- Находим среднее арифметическое (в квадратных метрах) большего и меньшего действующих значений основания. Складываем и делим на два.
- Измеряем в метрах, чтобы умножить высоту на среднюю площадь дна емкости.
Полученное значение — это объем объемного контейнера.
Для эллипсной бочки расчет производится по-другому.
- Измеряем расстояние между противоположными точками емкости, находящимися на эллиптическом (овальном) поперечном сечении. Получим два несоразмерных значения.
- Узнаем среднее арифметическое значений и делим его пополам, что даст радиус.
- Измеряем высоту и умножаем на квадрат среднего радиуса и π. Полученное значение — это объем овальной емкости в кубах.
Хотя термин «радиус» не совсем применим к овалу, его можно определить как среднюю величину. Намекается, что овал является представлением полностью симметричной кривой, которая выглядит как одновременно сплюснутый и вытянутый круг.
Прямоугольные емкости, внутреннее пространство которых представляет собой параллелепипед, вычисляются по объему быстрее, чем круглые образцы. Достаточно перемножить длину, ширину и высоту контейнера.
Объем в литрах
Для вычисления литража важно помнить о постоянной величине: 1 литр воды равен 0,001 кубическому метру. Стандартный центнер воды занимает 0,1 кубометра. Это правило применимо для всех жидкостей: один литр — это кубический дециметр. Например, для цистерны, вмещающей 4 тонны воды, расчет довольно прост — это такое же значение в кубах. В отличие от этого, например, 1 куб нефти будет весить значительно меньше одной тонны. Плотность нефти ниже плотности воды, что объясняет, почему вес определенного объема нефти меньше, чем вес такого же количества воды. Но величина 1 кубометр является постоянной.
Например, контейнер для полива огорода, который требует подключения поливных труб или патрубков для шлангов, имеет объем 200 литров, что соответствует 0,2 кубометра. Для вычисления используется та же формула перевода литров в кубометры.
Таким образом, для хранения одной тонны воды (1 м³) потребуется 5 таких контейнеров.
Баррель и его формулы
В работе калькулятора используются математические формулы для нахождения общего объема цилиндрического объекта в литрах и галлонах. Формула объема бочки будет продемонстрирована в практическом примере.
Пошаговый расчет может быть полезен для понимания того, как используются данные в математической формуле для нахождения объема бочки в литрах. Эти расчеты помогут определить объем цилиндрического тела.
Имеется цилиндрический объект со средним радиусом D = 18 дюймов, верхним и нижним радиусом d = 15 дюймов и высотой h = 10 дюймов. Поставленный вопрос: каков объем этого предмета?
- средний радиус D = 18 дюймов;
- верхний и нижний радиус d = 15 дюймов;
- высота h = 10 дюймов.
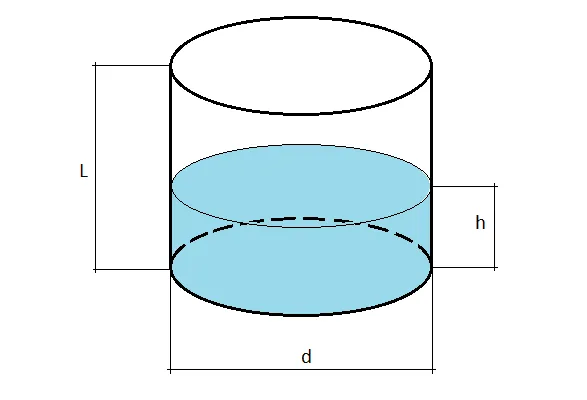
Расчет объема жидкости в неполной бочке
Пожалуйста, укажите размеры в миллиметрах.
D – диаметр емкости; H – уровень жидкости; L – высота бочки.
Программа произведет расчет объема жидкости в бочке, общего и свободного объемов, а также площадей поверхностей.
Если вам нужно рассчитать объем, радиус или высоту любого цилиндрического объекта, будь то бочка, труба, ведро, банка, колодец, бак и так далее — этот калькулятор объема цилиндра как раз для вас.
Принцип работы: 1. Выберите тип расчета (расчет объема цилиндра через радиус и высоту, расчет объема через площадь основания и высоту, расчет радиуса через объем и высоту, расчет высоты цилиндра через радиус цилиндра и объем) 2. Укажите два соответствующих параметра и выберите, в какой единице измерения вони заданы; 3. Укажите, в какой единице измерения вас интересует ответ; 4. Укажите количество цифр после запятой; 5. Нажмите кнопку «Расчет». Результат будет отображен ниже в указанной вами единице измерения.
— число Пи принято равным 3,141592653589793— формула объема цилиндра — V = 3,14 * H * R * R (где 3,14 — число Пи, H — высота цилиндра, R — радиус цилиндра) — если вам необходим более общий расчет объемов определенных фигур, воспользуйтесь следующим калькулятором.
От автора: Если данный калькулятор объема цилиндра оказался для вас полезным, не забудьте поделиться им с друзьями и коллегами, а также помните, что на сайте имеется большое количество других полезных калькуляторов. На разработку сервиса бесплатных строительных калькуляторов было потрачено очень много времени и усилий, поэтому любая поддержка проекта поможет мотивировать нас на создание более качественных и удобных инструментов для расчетов.
ЦИЛИНДРИЧЕСКИЕ ЕМКОСТИ
Цилиндрические емкости могут быть установлены как в горизонтальном, так и в вертикальном положении. Объем рассчитывается по формуле V = πr²h, что означает, что мы умножаем число π (примерно равное 3,14159) на квадрат радиуса и на высоту h цилиндра.
На примере: имеем вертикальный цилиндрический резервуар диаметром 3 метра и высотой 5 метров. Рассчитаем объем: радиус равен 1,5 метра, квадрат этого значения равен 2,25. Умножаем: 3,14159 × 2,25 × 5 (высота) = 35,34 м³. Таким образом, рабочий объем нашего резервуара составит 35 кубических метров или 35 000 литров (в одном кубе содержится 1000 литров).
На практике размеры резервуара рассчитываются с учетом его функциональности. Например, горизонтальный резервуар с диаметром 1 метр и длиной 10 метров будет неэффективен в использовании. Его объем составит 7,8 кубических метра. Если нам нужен резервуар такого объема, лучше увеличить его диаметр и уменьшить длину: например, выбрать диаметр 2 метра и длину 3 метра. Тогда получим тот же объем — 7,8 куба — при гораздо более удобных размерах.
ПРЯМОУГОЛЬНЫЕ ЕМКОСТИ
Для таких емкостей расчет еще проще. Чтобы определить общий объем, достаточно умножить длину на ширину и высоту. Например, кубический резервуар со стороной 1 метр содержит 1 куб жидкости. Резервуар размером 3000 мм × 2000 мм × 2500 мм будет иметь объем 15 кубометров.
Почему большинство резервуаров имеют не квадратную или прямоугольную, а цилиндрическую форму? Цилиндрические конструкции оказались более прочными. Чтобы сварить куб, потребуются 6 листов стали и 12 сварных швов. В отличие от этого, цилиндрическая емкость имеет всего 3 стороны: два круглых дна и цилиндрическую оболочку.
Корпус может быть выполнен из одного листа металла, свернутого в цилиндр, что потребует всего 1 сварного шва. И еще два круговых шва, чтобы приварить дны. В итоге, в идеальном варианте всего 3 сварных шва — вместо 12 у куба.
Почему же тогда делают прямоугольные емкости? У таких конструкций есть свои области применения. Например, они используются как пожарные резервуары — обладают отличной эргономикой и имеют возможность занимать минимум пространства в помещениях.
В нашей компании вы можете заказать резервуар практически любого типа, формы и назначения. Мы предлагаем как стандартные варианты, так и производим продукцию на заказ. Зная основные принципы расчета размеров и объемов резервуаров, вы сможете оценить, какой вариант окажется наиболее подходящим именно для вас.
Выберите подходящую емкость в нашем каталоге металлических изделий для различных задач.

Завод
Резервуарных
Конструкций
- info@zrk-1.ru
- Оставить заявку
Внутренний объем погонного метра трубы в литрах — таблица
Таблица отображает внутренний объем одного погонного метра трубы в литрах, то есть, сколько жидкости, такой как вода или антифриз, потребуется для заполнения трубопровода. При этом учитывается внутренний диаметр труб от 4 до 1000 миллиметров.
| Внутренний диаметр, мм | Внутренний объем 1 м погонного трубы, литров | Внутренний объем 10 м погонных труб, литров |
| 4 | 0.0126 | 0.1257 |
| 5 | 0.0196 | 0.1963 |
| 6 | 0.0283 | 0.2827 |
| 7 | 0.0385 | 0.3848 |
| 8 | 0.0503 | 0.5027 |
| 9 | 0.0636 | 0.6362 |
| 10 | 0.0785 | 0.7854 |
| 11 | 0.095 | 0.9503 |
| 12 | 0.1131 | 1.131 |
| 13 | 0.1327 | 1.3273 |
| 14 | 0.1539 | 1.5394 |
| 15 | 0.1767 | 1.7671 |
| 16 | 0.2011 | 2.0106 |
| 17 | 0.227 | 2.2698 |
| 18 | 0.2545 | 2.5447 |
| 19 | 0.2835 | 2.8353 |
| 20 | 0.3142 | 3.1416 |
| 21 | 0.3464 | 3.4636 |
| 22 | 0.3801 | 3.8013 |
| 23 | 0.4155 | 4.1548 |
| 24 | 0.4524 | 4.5239 |
| 26 | 0.5309 | 5.3093 |
| 28 | 0.6158 | 6.1575 |
| 30 | 0.7069 | 7.0686 |
| 32 | 0.8042 | 8.0425 |
| 34 | 0.9079 | 9.0792 |
| 36 | 1.0179 | 10.1788 |
| 38 | 1.1341 | 11.3411 |
| 40 | 1.2566 | 12.5664 |
| 42 | 1.3854 | 13.8544 |
| 44 | 1.5205 | 15.2053 |
| 46 | 1.6619 | 16.619 |
| 48 | 1.8096 | 18.0956 |
| 50 | 1.9635 | 19.635 |
| 52 | 2.1237 | 21.2372 |
| 54 | 2.2902 | 22.9022 |
| 56 | 2.463 | 24.6301 |
| 58 | 2.6421 | 26.4208 |
| 60 | 2.8274 | 28.2743 |
| 62 | 3.0191 | 30.1907 |
| 64 | 3.217 | 32.1699 |
| 66 | 3.4212 | 34.2119 |
| 68 | 3.6317 | 36.3168 |
| 70 | 3.8485 | 38.4845 |
| 72 | 4.0715 | 40.715 |
| 74 | 4.3008 | 43.0084 |
| 76 | 4.5365 | 45.3646 |
| 78 | 4.7784 | 47.7836 |
| 80 | 5.0265 | 50.2655 |
| 82 | 5.281 | 52.8102 |
| 84 | 5.5418 | 55.4177 |
| 86 | 5.8088 | 58.088 |
| 88 | 6.0821 | 60.8212 |
| 90 | 6.3617 | 63.6173 |
| 92 | 6.6476 | 66.4761 |
| 94 | 6.9398 | 69.3978 |
| 96 | 7.2382 | 72.3823 |
| 98 | 7.543 | 75.4296 |
| 100 | 7.854 | 78.5398 |
| 105 | 8.659 | 86.5901 |
| 110 | 9.5033 | 95.0332 |
| 115 | 10.3869 | 103.8689 |
| 120 | 11.3097 | 113.0973 |
| 125 | 12.2718 | 122.7185 |
| 130 | 13.2732 | 132.7323 |
| 135 | 14.3139 | 143.1388 |
| 140 | 15.3938 | 153.938 |
| 145 | 16.513 | 165.13 |
| 150 | 17.6715 | 176.7146 |
| 160 | 20.1062 | 201.0619 |
| 170 | 22.698 | 226.9801 |
| 180 | 25.4469 | 254.469 |
| 190 | 28.3529 | 283.5287 |
| 200 | 31.4159 | 314.1593 |
| 210 | 34.6361 | 346.3606 |
| 220 | 38.0133 | 380.1327 |
| 230 | 41.5476 | 415.4756 |
| 240 | 45.2389 | 452.3893 |
| 250 | 49.0874 | 490.8739 |
| 260 | 53.0929 | 530.9292 |
| 270 | 57.2555 | 572.5553 |
| 280 | 61.5752 | 615.7522 |
| 290 | 66.052 | 660.5199 |
| 300 | 70.6858 | 706.8583 |
| 320 | 80.4248 | 804.2477 |
| 340 | 90.792 | 907.9203 |
| 360 | 101.7876 | 1017.876 |
| 380 | 113.4115 | 1134.1149 |
| 400 | 125.6637 | 1256.6371 |
| 420 | 138.5442 | 1385.4424 |
| 440 | 152.0531 | 1520.5308 |
| 460 | 166.1903 | 1661.9025 |
| 480 | 180.9557 | 1809.5574 |
| 500 | 196.3495 | 1963.4954 |
| 520 | 212.3717 | 2123.7166 |
| 540 | 229.0221 | 2290.221 |
| 560 | 246.3009 | 2463.0086 |
| 580 | 264.2079 | 2642.0794 |
| 600 | 282.7433 | 2827.4334 |
| 620 | 301.9071 | 3019.0705 |
| 640 | 321.6991 | 3216.9909 |
| 660 | 342.1194 | 3421.1944 |
| 680 | 363.1681 | 3631.6811 |
| 700 | 384.8451 | 3848.451 |
| 720 | 407.1504 | 4071.5041 |
| 740 | 430.084 | 4300.8403 |
| 760 | 453.646 | 4536.4598 |
| 780 | 477.8362 | 4778.3624 |
| 800 | 502.6548 | 5026.5482 |
| 820 | 528.1017 | 5281.0173 |
| 840 | 554.1769 | 5541.7694 |
| 860 | 580.8805 | 5808.8048 |
| 880 | 608.2123 | 6082.1234 |
| 900 | 636.1725 | 6361.7251 |
| 920 | 664.761 | 6647.6101 |
| 940 | 693.9778 | 6939.7782 |
| 960 | 723.8229 | 7238.2295 |
| 980 | 754.2964 | 7542.964 |
| 1000 | 785.3982 | 7853.9816 |
Способы перевода кубометров в другие кубические единицы
При расчете объемов необходимо придерживаться единых единиц измерения. Если ваши данные представлены в различных единицах, а конечный результат требуется в кубометрах, достаточно провести правильные преобразования.
Если V измеряется в мм³, см³, дм³ или литрах, то переводим эти величины в м³ следующим образом:
- 1 м³ = 1 мм³ × 0,000000001 = 1 мм³ × 10⁻⁹;
- 1 м³ = 1 см³ × 0,000001 = 1 см³ × 10⁻⁶;
- 1 м³ = 1 дм³ × 0,001 = 1 дм³ × 10⁻³. Этот же перевод применяется для литров, так как в 1 литре содержится 1 дм³.
Чтобы получить кубы вещества, зная его массу, необходимо либо обратить внимание на таблицы с его плотностью, либо определить плотность вручную. Чтобы найти V материала (в м³), нужно массу М (кг) разделить на плотность Р (кг/м³).
Подсчитать кубические метры не представляет особой сложности для человека, не обладающего математическими склонностями, хотя в каждом случае требуется индивидуальный подход.
Знания по определению объемов нужны не только специалистам, но и простым людям в повседневной жизни.
- https://ru.onlinemschool.com/math/formula/volume/
- https://exceltut.ru/formuly-obema-geometricheskih-figur-najti-vse-obemy/
- https://zametkiddach.ru/obem-bochki-kalkulyator
- https://iobogrev.ru/rasschitat-obem-baka-v-litrah-po-razmeram
- https://StroySoveti.ru/kanalizaciya/kak-rasschitat-obem-emkosti-razlichnoy-formyi.html
- https://VseProTruby.ru/vodoprovodnye/raschet-obema-vody-v-trube.html
- http://LediZnaet.ru/deti/mir-znanij/kak-poschitat-obyom.html
- Поднимите комфорт в гостиной: очарование угловых диванов.
- Обеспечение стабильного электроснабжения: исследование однофазных стабилизаторов напряжения наружной установки.
- Корпоративная пенсионная программа.
- Проекты домов из бруса 6х6.
- ТопКровля: Ваш надежный партнер по кровельным и фасадным решениям в Волгодонске и Ростове-на-Дону.
- Эволюция управления строительством: вектор на автоматизацию.
- Оптимизация энергопотребления: новые горизонты и методы.








