Термин «диаметр» охватывает как отрезок, который соединяет две противоположные точки окружности и проходит через центр, так и длину этого отрезка. Диаметр присущ любому круглому объекту, будь то озеро, мяч, печенье или даже радуга; если представить, что радуга образует полный круг, мы видим лишь её часть.
Калькулятор диаметра
Используйте калькулятор, чтобы рассчитать диаметр круга, основываясь на длине окружности, радиусе или площади круга.
Содержание:
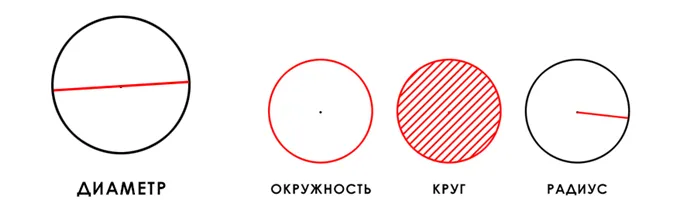
Диаметр круга — это отрезок, соединяющий две точки на окружности и одновременно проходящий через центр круга.
Что касается других геометрических форм, то максимальное расстояние между двумя точками таких фигур также называют диаметром. Это положение верно и для круга, поскольку диаметр этого геометрического объекта представляет собой самый длинный отрезок, который может быть проведён в пределах окружности.
Если нарисовать диаметр, он будет представлен на следующем изображения (выделен красным цветом на картинке ниже).
Теперь обратим внимание на способы, с помощью которых можно определить диаметры и соответствующие формулы для вычислений.
Формулы определения диаметра круга
Существуют различные методы для нахождения диаметра, которые зависят от известных параметров круга.
По радиусу
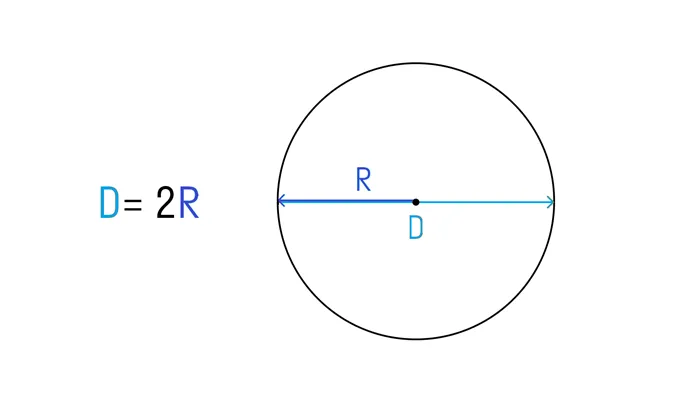
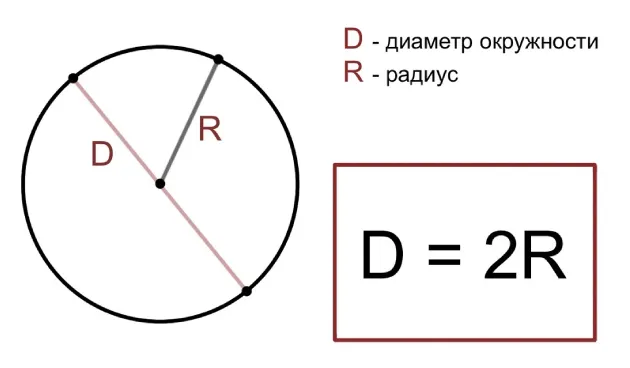
Самая простая формула для определения диаметра применяется, когда известен радиус круга. Радиус — это отрезок от центра окружности до любой точки на её границе. Соотношение заключается в том, что диаметр равен удвоенному радиусу.
Формула выглядит следующим образом: d = 2r, где d — это диаметр, а r — радиус.
По длине окружности
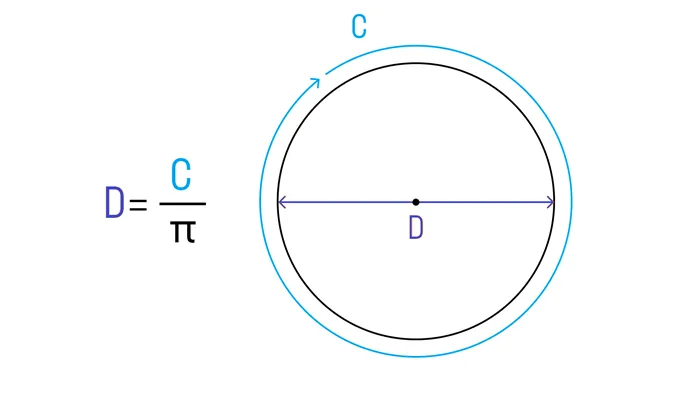
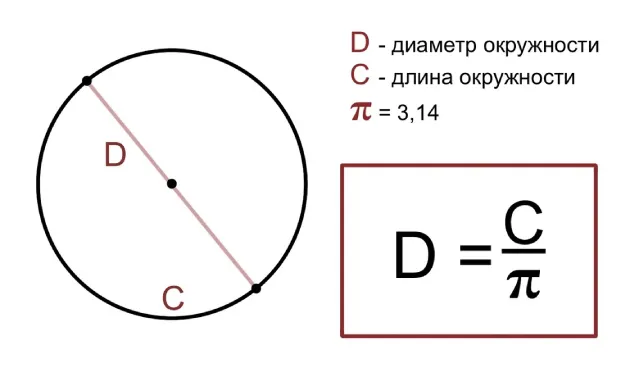
Метод нахождения диаметра по длине окружности подходит, когда известна длина окружности. Окружность — это замкнутая кривая, состоящая из всех точек, равноудалённых от центра. Здесь диаметр равен длине окружности, делённой на число Пи.
Формула представлена так: d = L / π, где d — это диаметр, L — длина окружности, а π — математическая константа, примерно равная 3,14.
Данная формула основывается на принципе, что отношение длины окружности к её диаметру остаётся постоянным, равно как число π.
Через площадь круга
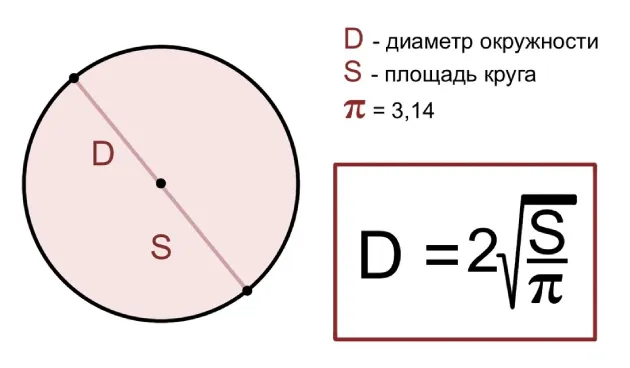
Формула определения диаметра через площадь круга немного сложнее. Чаще всего необходимо найти площадь, зная диаметр, но если задача состоит в обратном, то применяется следующая формула:
d = 2 * √(S / π), где d — это диаметр, S — площадь круга, а π — константа, равная примерно 3,14.
Таким образом, диаметр соответствует удвоенному квадратному корню из отношения площади круга к числу пи. Важно заметить, что корень и степень ½ эквивалентны.
Основные понятия
Диаметр — это отрезок, который проходит через центр окружности и соединяет две противоположные точки на её границе, а также длина этого отрезка. Обозначается как d.
Окружность — это фигура, состоящая из всех точек плоскости, находящихся на равном расстоянии от центра. Длина окружности обозначается как l.
Круг — это плоская геометрическая фигура, ограниченная окружностью. Площадь круга обозначается Sк.
Радиус — это отрезок, соединяющий центр окружности с любой точкой на ней. Обозначается как r.
Число Пи — это математическая константа, представляющая иррациональное число, показывающее отношение длины окружности к её диаметру, приближенно равное 3,1415 и обозначаемое как π.
Формула диаметра окружности
Для вычисления диаметра окружности существуют различные методы, в зависимости от доступных данных: можно использовать радиус окружности, её длину, или площадь круга.
Через радиус окружности (R)
Радиус окружности — это расстояние от её центра до любой точки на границе. Поскольку диаметр проходит через центр и соединяет две точки на границе, он в два раза больше радиуса. Таким образом, формула для расчёта диаметра через радиус будет выглядеть следующим образом:
d = 2r, где d — это диаметр, r — радиус окружности.
По длине окружности (l)
Длина окружности может быть выражена через диаметр и число Пи. Чтобы найти диаметр, основываясь на длине окружности, нужно разделить длину окружности на число Пи:
d = l / π, где d — это диаметр, l — длина окружности.
Через площадь круга S
Площадь круга определяется как квадрат радиуса, умноженный на число Пи. Чтобы выразить диаметр через площадь, необходимо сначала найти радиус, а затем подставить его в соответствующую формулу.
Формула для нахождения диаметра выглядит следующим образом:
d = 2 * √(S / π), где d — диаметр, S — площадь круга.
Помочь в учебе может подходящий ноутбук или планшет.
Ноутбук или планшет можно приобрести в кредит. В этом случае удобно использовать кредитную карту с длительным льготным периодом без процентов. Вот несколько предложений таких карт:
Платинум от Т-Банка предлагает 55 дней без процентов.
Год без процентов от Альфа-Банка предоставляет до 365 дней льготного периода, а также возможность снятия наличных до 100 000 рублей без комиссии.
MTS Cashback от МТС Банка предлагает до 111 дней льготного периода с бонусом кэшбэка в 5% на покупки в супермаркетах.
Своя кредитка от Своего Банка предусматривает до 120 дней без процентов.
Дополнительно, можно накопить на покупку, используя накопительный счёт или вклад, не выходя из дома.
Условия по продуктам актуальны на момент публикации материала.
Полезная информация о диаметре окружности
| В окружности можно провести бесконечное количество диаметров | Поскольку окружность состоит из бесконечного множества точек, каждая из которых может быть концом отрезка-диаметра. |
| Диаметр всегда проходит через центр окружности | Кроме того, окружность делится диаметром пополам. |
| Слово «диаметр» происходит из древнегреческого языка | От διάμετρος, что означает «поперечник», где διά переводится как «через; раздельно» и μετρέω — «измеряю». |
| От термина диаметр образовано наречие «диаметрально» | Это слово означает «полностью» или «абсолютно» и чаще всего используется в контексте выражения «диаметрально противоположный». |
Диаметр, как геометрическая величина, может быть выражен через другие параметры, связанные с окружностью и её фигурами. Теперь рассмотрим формулы, которые чаще всего применяются для вычисления диаметра.
Через длину окружности
Через радиус окружности
Связь между диаметром и радиусом окружности самая простая: фактически, диаметр равен удвоенному радиусу, который располагается на одной прямой. Это позволяет легко сформулировать формулу для вычисления диаметра через радиус: нужно умножить его на два.
Через площадь круга
Диаметр может вычисляться не только через численные параметры самой окружности, но и через площадь площади круга, ограниченного ей.
Построение диаметра с помощью циркуля и линейки
Для того чтобы построить диаметр окружности, необходимо провести прямую линию через её центр. Однако не всегда мы знаем, где точно находится этот центр.
Например, как узнать диаметр круглой тарелки без штангенциркуля? В этом случае может помочь простой способ построения диаметра с использованием обычного циркуля и линейки.
Допустим, мы положили тарелку на лист бумаги и обвели её карандашом, получив окружность. Как же измерить её диаметр, имея под рукой только циркуль и линейку? Если попытаться провести диаметр на глаз, есть риск получить отрезок, близкий по длине к диаметру, но не совпадающий с ним. Поэтому воспользуемся простым и точным методом построения диаметра.
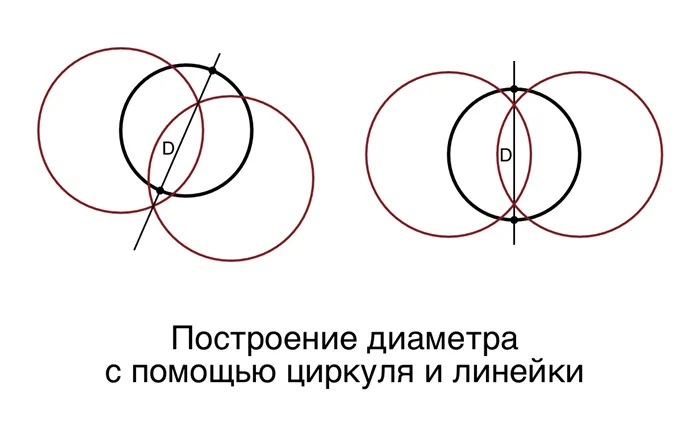
Для этого нужно начертить две окружности, центры которых будут находиться по обе стороны от уже нарисованной окружности, причём их диаметры должны превышать диаметр исходной окружности. Затем необходимо провести прямую линию через точки их пересечения, которые могут находиться вне исходной окружности. Отрезок этой прямой линии, который располагается внутри первой окружности, и будет её диаметром.
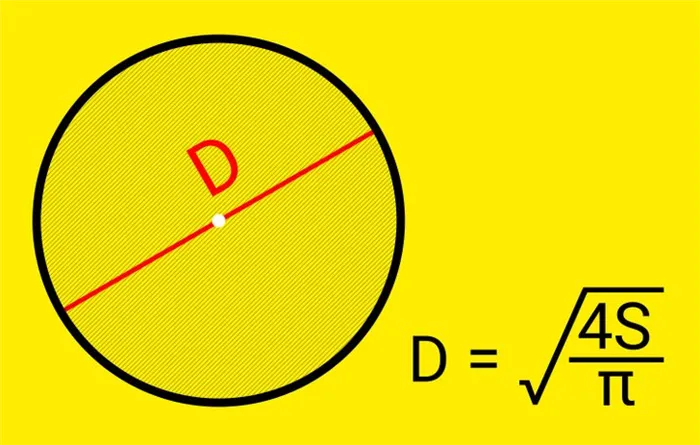
Как найти диаметр, если известна площадь
Если площадь круга известна, диаметр можно вычислить следующим образом: умножьте площадь на 4, разделите полученное значение на число Пи (что приблизительно равно 3,14), а затем извлеките корень из результата.
❗Обратите внимание, полученный результат не будет абсолютно точным, поскольку значение числа Пи приближённое.
Предположим, площадь нашего круга составила 20 см². В этом случае 20 * 4 / 3,14 = 25,48. Используя калькулятор, извлекаем корень из этого числа. Таким образом, диаметр круга составит примерно 5,05 см.
Как найти диаметр, если другие параметры неизвестны
Если у вас нет информации о каких-либо параметрах окружности, но имеется её чертёж, попробуйте измерить диаметр с помощью линейки. Для этого определите центр окружности, проведите через него линию от одного края до другого и измерьте её длину.
✅ Простейший способ найти центр окружности — это начертить квадрат вокруг неё, а затем провести его диагонали, соединяя противоположные углы квадрата. То место, где эти диагонали пересекаются, будет центром окружности.
Что такое калькулятор для вычисления диаметра через длину окружности
Онлайн калькулятор для нахождения диаметра через длину окружности — это инструмент, разработанный для быстрого и удобного расчета диаметра окружности на основе заданных данных о длине. Этот калькулятор окажется полезным для решения задач, связанных с геометрией и инженерными изысканиями. Независимо от того, ведётся ли речь о проектировании круглых объектов, архитектурных разработках или задачах из области физики, калькулятор диаметра станет вашим надёжным помощником.
Пример 1: Расчёт диаметра по длине окружности
Предположим, у нас есть окружность с длиной \( L = 10 \) метров. Мы хотим узнать, каков будет диаметр этой окружности.
Шаги:
- Введите значение длины окружности: \( L = 10 \).
- Нажмите кнопку “Разберись”.
- Получите результат: Диаметр окружности составит примерно \( \approx 3,183 \) метра.
Таким образом, калькулятор демонстрирует быструю и удобную возможность определения диаметра окружности, основываясь на заданной длине.
Пример 2: Расчёт диаметра для архитектурных целей
Представим, что вы проектируете круглый фонтан с определённой длиной окружности. В этом случае необходимо быстро и точно рассчитать соответствующий диаметр.
Шаги:
- Введите значение длины окружности: \( L = 15 \) метров.
- Нажмите кнопку “Разберись”.
- Получите результат: Диаметр окружности будет примерно \( \approx 4,774 \) метра.
Таким образом, калькулятор позволяет эффективно решать практические задачи при проектировании архитектурных объектов.
Как пользоваться калькулятором
- Введите значение длины окружности в соответствующее поле для данных.
- Нажмите кнопку “Разберись”, чтобы калькулятор провёл расчёт.
- Получите мгновенный и точный ответ, представленный в виде диаметра окружности.
С помощью онлайн калькулятора для вычисления диаметра через длину окружности вы сможете быстро и эффективно решать задачи, связанные с геометрией и проектированием. Простой интерфейс и мгновенные результаты делают этот калькулятор незаменимым инструментом в вашей работе.
Часы работы службы поддержки:
ПН-ПТ: 10:00 — 19:30