Если вычисления производятся в сантиметрах, то результат дается в кубических сантиметрах. Должно быть понятно, что между кубическими сантиметрами и литрами существует четкая взаимосвязь. Конвертация осуществляется путем деления полученного значения объема на 1000. После этого данные выражаются в литрах.
Формулы, позволяющие находить объём цилиндра в метрах и литрах
Среди множества геометрических фигур часто встречается цилиндр. Это геометрическое тело используется в многочисленных расчетах. Согласно принятой терминологии, этот термин относится к геометрическому телу, имеющему поверхность в основании. Эта поверхность также имеет форму цилиндра.
В литературе эту поверхность часто называют боковой поверхностью. Кроме того, эта форма имеет пару граней, называемых основаниями. Эти основания цилиндра представляют собой круги с одинаковым диаметром. Цилиндр с окружностью в основании называется круговым.
Со школьных времен все знают форму цилиндра классического типа. Это круговой цилиндр.
Типы цилиндров
В математике существует несколько типов цилиндров, которые постоянно используются в геометрии.
- Цилиндр прямого типа. Это геометрическая фигура, которая имеет прямой угол между боковой поверхностью и основаниями. Такой тип самый распространённый и часто применяется в решении большого количества задач.
- Наклонный цилиндр. Исходя из основания фигуры, можно сделать вывод, что угол между боковой поверхностью и основаниями фигуры будет отличным от прямого. При этом он может колебаться в своём значении, как в большую, так и в меньшую сторону от прямого угла.
Вычисление объёма
При работе с цилиндрами часто возникает необходимость вычислить их объем. В последнее время этот процесс осуществляется с помощью компьютерных технологий. Однако, чтобы осуществить такой процесс, не обязательно использовать калькулятор и другие дополнительные методы решения задачи.
В настоящее время существует несколько основных методов, позволяющих рассчитать данный параметр. По сути, это универсальные формулы. Каждая из этих формул имеет свои входные параметры, на основании которых можно определить нужное значение объема. Это оказывает несколько положительных эффектов на вычисления.
- Значительно сокращается время для осуществления операций подсчёта объёма.
- Уменьшается вероятность того что может быть совершена ошибка в расчётах
- Требуется для вычисления ограниченное число параметров, знание которых и даёт возможность достигать результата.

Как найти объем цилиндра
wikiHow работает по принципу вики, что означает, что многие наши статьи написаны более чем одним автором. На момент написания статьи над редактированием и улучшением этой статьи работали 38 человек, некоторые из них анонимно.
Количество просмотров этой статьи: 71 756.
Цилиндр — это объемная геометрическая фигура с параллельными круговыми основаниями. Чтобы определить объем цилиндра, найдите высоту (h) и радиус основания (r) и подставьте их в формулу: V = hπr 2 .
Нахождение объема цилиндра
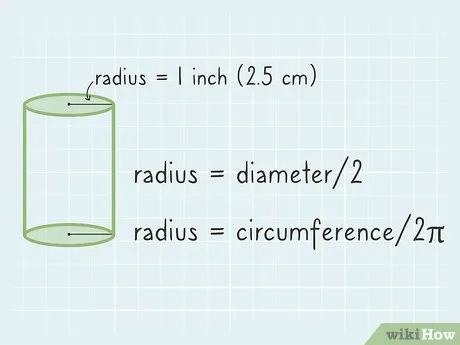
- Если дан диаметр, разделите его на 2 и получите радиус.
- Если дана длина окружности, разделите ее на 2π и получите радиус.
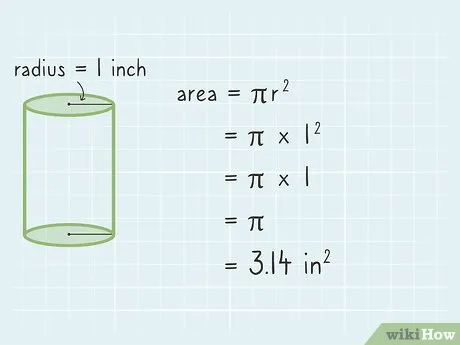
- A = π x 1 2 =
- A = π x 1.
- Так как π ≈ 3,14, то площадь основания равна 3,14 см 2 .

Найдите высоту цилиндра. Если она задана, переходите к следующему шагу. В противном случае измерьте высоту линейкой. Высота — это расстояние между двумя основаниями. Например, высота равна 4 см.

- Объем измеряется в кубических единицах, так как это величина, характеризующая объемные (трехмерные) фигуры.
- Придумайте несколько задач и попрактикуйтесь.
- Измеряйте все точно.
- Проще воспользоваться калькулятором.
- Помните: диаметр – наибольшее расстояние между двумя точками на окружности. Так что прижмите точку начала отсчета линейки к краю цилиндра и найдите самое большое расстояние до другого края. Это и будет диаметр.
- В общих случаях объем всегда равен произведению площади основания фигуры на ее высоту (это не работает в некоторых случаях, например, в конусе).
- Для получения радиуса проще найти диаметр и разделить его на два.
- Объем цилиндра вычисляется по формуле: V = πr 2 h.
- Перемножение площади основания и его высоты аналогично сложению множества его оснований (представьте прозрачный цилиндр, наполненный его основаниями).
Дополнительные статьи

Об этой статье
wikiHow работает по принципу вики, что означает, что многие наши статьи написаны более чем одним автором. Когда эта статья была создана, над ее редактированием и улучшением работали 38 человек, в том числе анонимно. Количество просмотров этой статьи: 71 756
Cookies помогают сделать WikiHow лучше. Если вы продолжаете пользоваться нашим сайтом, вы соглашаетесь с нашими условиями использования файлов cookie.
🧮 Что такое калькулятор объема цилиндра?
Калькулятор объема цилиндра — это инструмент, который позволяет автоматически вычислить объем цилиндра по его размерам. Калькулятор объема цилиндра обычно предоставляет пользователю простую форму для ввода радиуса основания и высоты цилиндра, а затем нажмите кнопку «Рассчитать». Калькулятор объема цилиндра может быть предложен в виде программы на компьютере или мобильном устройстве или в виде веб-сервиса на сайте, подобном нашему.
Использование калькулятора объема цилиндра упрощает и ускоряет вычисление объема цилиндра, особенно когда необходимо вычислить объем нескольких цилиндров или когда радиус и высота цилиндра имеют сложные числовые значения. Калькулятор объема цилиндра может быть полезен в различных областях, таких как наука, машиностроение, строительство, производство, образование и домашнее хозяйство.
📏 Как работает калькулятор объема цилиндра?
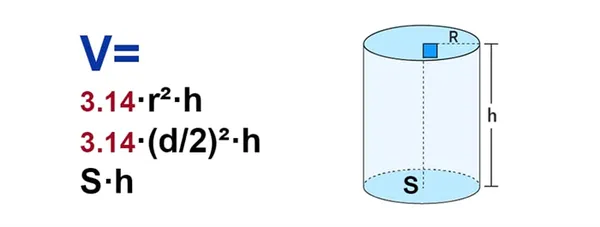
Калькулятор объема цилиндра работает на основе математической формулы для вычисления объема цилиндра, описанной выше.
Чтобы рассчитать объем цилиндра, пользователь должен ввести радиус основания и высоту цилиндра в соответствующие поля калькулятора и нажать кнопку «Рассчитать». Калькулятор использует введенные значения, выполняет математическую операцию по формуле и отображает результат в соответствующем поле на экране.
Некоторые калькуляторы объема цилиндра имеют дополнительные функции, такие как выбор единиц измерения (например, сантиметры или дюймы) и возможность рассчитать объем цилиндра, используя диаметр основания вместо радиуса.
🛢 Как использовать калькулятор объема цилиндра?
Выполните следующие простые шаги, чтобы воспользоваться калькулятором объема цилиндра:
- Откройте калькулятор объема цилиндра, который находится на компьютере, мобильном устройстве или на веб-сайте.
- Введите значение радиуса основания цилиндра в соответствующее поле калькулятора. Если вы используете калькулятор, который принимает во внимание диаметр, убедитесь, что вы выбрали правильную единицу измерения.
- Введите значение высоты цилиндра в соответствующее поле калькулятора. Убедитесь, что вы выбрали правильную единицу измерения.
- Нажмите кнопку «Рассчитать» или «Получить результат». Калькулятор выполнит расчеты и выведет объем цилиндра в соответствующем поле.
- Проверьте результаты и убедитесь, что все значения введены правильно и выбраны правильные единицы измерения.
- Если нужно рассчитать объем нескольких цилиндров, повторите шаги 2-5 для каждого цилиндра.
- Сохраните результаты или скопируйте их в буфер обмена, если нужно использовать их в другой программе или приложении.
В зависимости от характеристик калькулятор может иметь дополнительные функции, такие как выбор единиц измерения, возможность использовать диаметр вместо радиуса, а также возможность сохранить результаты в файл или отправить их по электронной почте.
Нахождение объема цилиндра: формула и задачи
В этой статье мы рассмотрим, как можно найти объем цилиндра, и рассмотрим несколько примеров.
Через площадь основания и высоту
Объем (V) цилиндра равен произведению его высоты и площади основания.
V = S ⋅ H
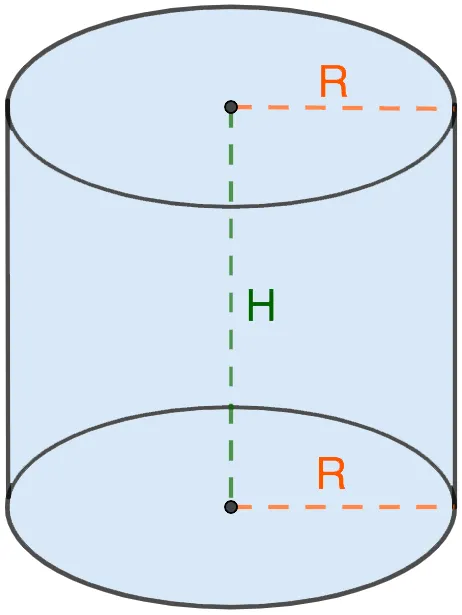
Через радиус основания и высоту
Как известно, основания цилиндра (равные друг другу) образуют круг, площадь которого вычисляется как S = π ⋅ R 2
V = π ⋅ R 2 ⋅ H
Примечание: В расчетах значение π округлено до 3,14.
Через диаметр основания и высоту
Как известно, диаметр круга равен двум его радиусам: d = 2R . Поэтому вычислите объем цилиндра следующим образом:
Примеры задач
Задача 1 Определите объем цилиндра, если его основание равно 78,5 см2 , а высота 10 см.
Решение.
Задача 2 Высота цилиндра равна 6 см, а его диаметр — 8 см. Найдите объем фигуры.
Решение.
Публикации по теме:
- Нахождение площади круга: формула и примеры
- Нахождение площади ромба: формула и примеры
- Нахождение площади трапеции: формула и примеры
- Нахождение площади параллелограмма: формула и примеры
- Нахождение периметра треугольника: формула и задачи
- Нахождение периметра прямоугольника: формула и задачи
- Нахождение периметра ромба: формула и задачи
- Теорема синусов для треугольника: формула и задачи
- Теорема о сумме углов треугольника: формула и задачи
- Нахождение объема куба: формула и задачи
- Нахождение объема шара: формула и задачи
- Нахождение объема пирамиды: формула и задачи
- Нахождение площади поверхности куба: формула и задачи
- Нахождение радиуса шара: формула и примеры
- Нахождение радиуса круга: формула и примеры
- Нахождение площади правильной призмы: формула и задачи
- Формула Герона для треугольника
- Теорема Менелая: формулировка и пример с решением
- Теорема Фалеса: формулировка и пример решения задачи
- Свойства равнобедренного треугольника: теория и задача
- Свойства равностороннего треугольника: теория и пример задачи
- Определение и свойства биссектрисы угла треугольника
- Свойства биссектрисы равнобедренного треугольника
- Формулы для нахождения высоты треугольника
- Свойства высоты равнобедренного треугольника
- Свойства высоты прямоугольного треугольника
- Что такое ромб: определение, свойства, признаки
- Нахождение радиуса вписанной в ромб окружности
- Что такое окружность: определение, свойства, формулы
- Что такое параллелограмм: определение, свойства, признаки
- Что такое трапеция: определение, виды, свойства
- Свойства равнобедренной (равнобокой) трапеции
- Что такое средняя линия треугольника
- Что такое шар (сфера): определение, свойства, формулы
- Нахождение площади шарового сегмента
- Что такое конус: определение, элементы, виды
- Основные свойства конуса
- Что такое усеченный конус: определение, основные элементы
- Что такое правильная пирамида: определение, виды, свойства
- Пирамида с перпендикулярным плоскости основания боковым ребром
- Что такое тетраэдр: определение, виды, формулы площади и объема
- Нахождение радиуса/площади/объема вписанного в конус шара (сферы)
- Нахождение радиуса/площади/объема описанной около конуса сферы (шара)
- Основные свойства эллипса
- Нахождение периметра эллипса
- Нахождение радиуса описанной вокруг правильного многоугольника окружности
- Нахождение радиуса вписанной в правильный многоугольник окружности
- Виды уравнений прямой с примерами (графиками)
- Что такое луч: определение, обозначение, признаки совпадения
- Что такое отрезок: определение, обозначение, свойства, взаимное расположение
Формула объема цилиндра через диаметр
К сожалению, бывает так, что при вычислении объема фигуры известны не все размеры. Например, радиус может быть неизвестен.
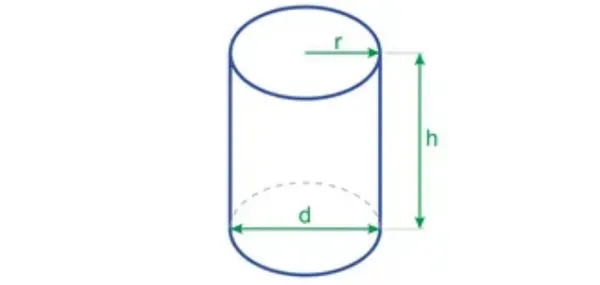
В этом случае, если вы знаете или можете измерить диаметр, можно воспользоваться следующей формулой:
Объем полого цилиндра
Расчет полого цилиндра необходим, например, если нужно вычислить массу полого тела. Масса равна произведению плотности материала и объема.
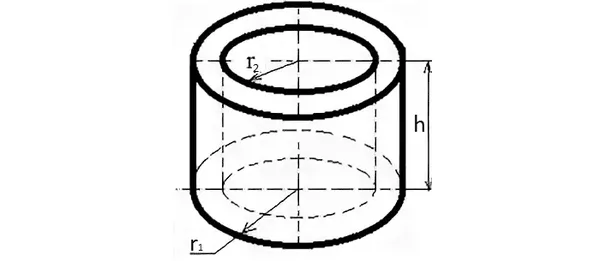
Формула для расчета выглядит следующим образом:
V = π (r 1 2 — r 2 2 )h
- r1 2 – внешний радиус;
- r2 2 – внутренний радиус;
- h – высота.
Примеры задач с решениями
Задача №1
Высота бочки с водой 3 м, ее радиус 0,75 м. Вычислите в литрах, сколько жидкости необходимо, чтобы заполнить бочку до середины?
Ответ.
Задача №2
В магазине приготовили пустой цилиндр. Диаметр дна равен высоте и составляет 20 см. Определите объем изделия.
Ответ: 100480 см3 .
Задача №3
В лаборатории необходимо изготовить две трубки с двумя одинаковыми поверхностями. Внешний радиус первой трубы равен 5 см, внутренний радиус равен 4 см, а высота равна 200 см. Внутренний радиус второй трубы равен 3 см.
Сколько материала необходимо для изготовления труб?